ACM Conference on Management of Data (SIGMOD)

Yaoshu Wang¹ Chuan Xiao² Jianbin Qin¹ Rui Mao¹ Makoto Onizuka² Wei Wang^4,5 Rui Zhang⁶ Yoshiharu Ishikawa³

¹Shenzhen University ²Osaka University ³Nagoya University ⁴Dongguan University of Technology ⁵University of New South Wales ⁶www.ruizhang.info

ABSTRACT

Selectivity estimation aims at estimating the number of database objects that satisfy a selection criterion. Answering this problem accurately and efficiently is essential to many applications, such as density estimation, outlier detection, query optimization, and data integration. The estimation problem is especially challenging for large-scale high-dimensional data due to the curse of dimensionality, the large variance of selectivity across different queries, and the need to make the estimator consistent (i.e., the selectivity is non-decreasing in the threshold). We propose a new deep learning based model that learns a query-dependent piecewise linear function as selectivity estimator, which is flexible to fit the selectivity curve of any distance function and query object, while guaranteeing that the output is non-decreasing in the threshold. To improve the accuracy for large datasets, we propose to partition the dataset into multiple disjoint subsets and build a local model on each of them. We perform experiments on real datasets and show that theproposedmodel consistently outperforms state-of-the-art models inaccuracy in an efficient way and is useful for real applications.

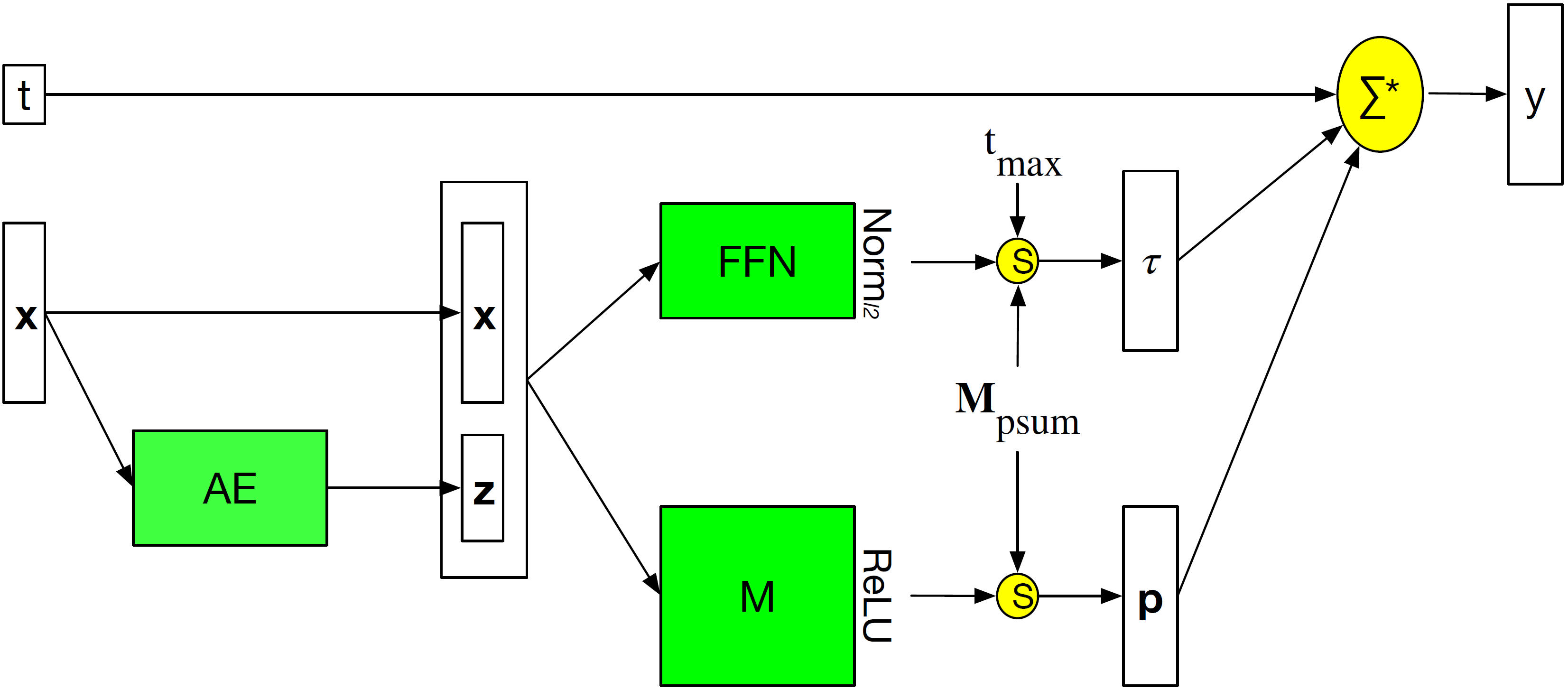
Figure 1: Network architecture.

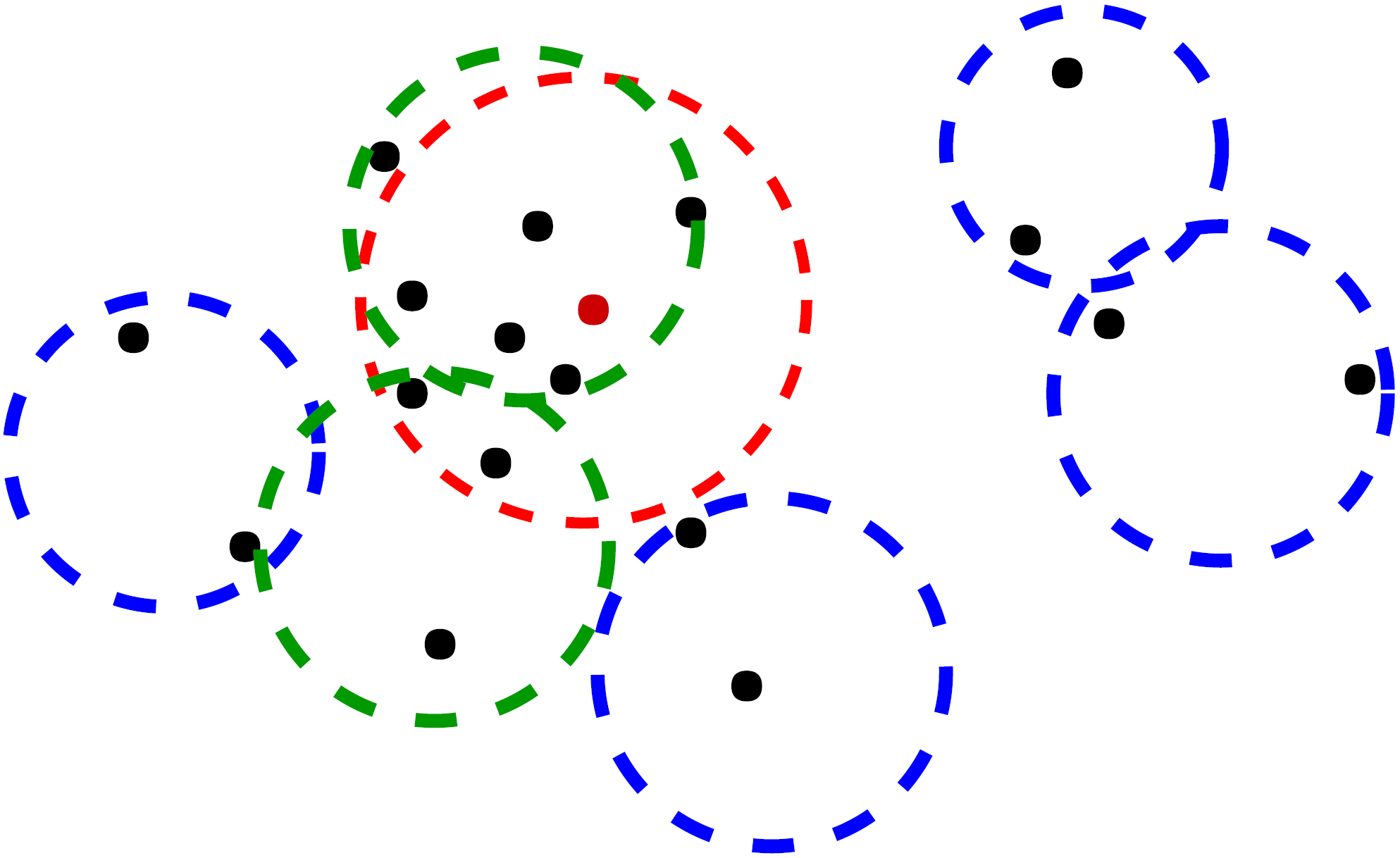
Figure 2: Data partitioning by cover tree

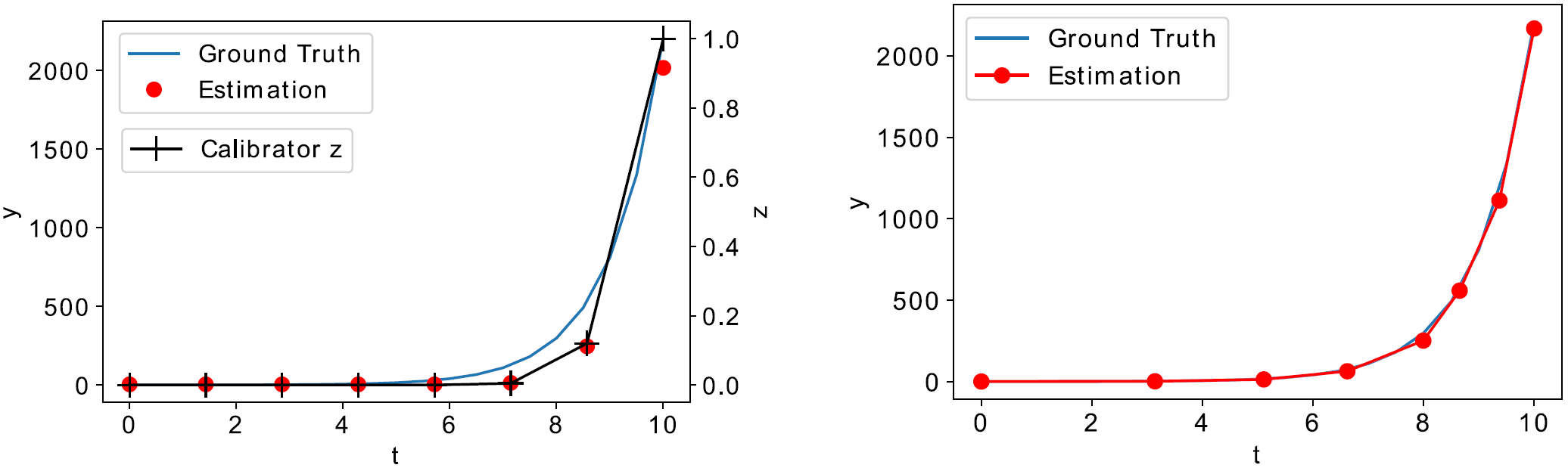
Figure 3: Comparison of simplified DLN and our model.

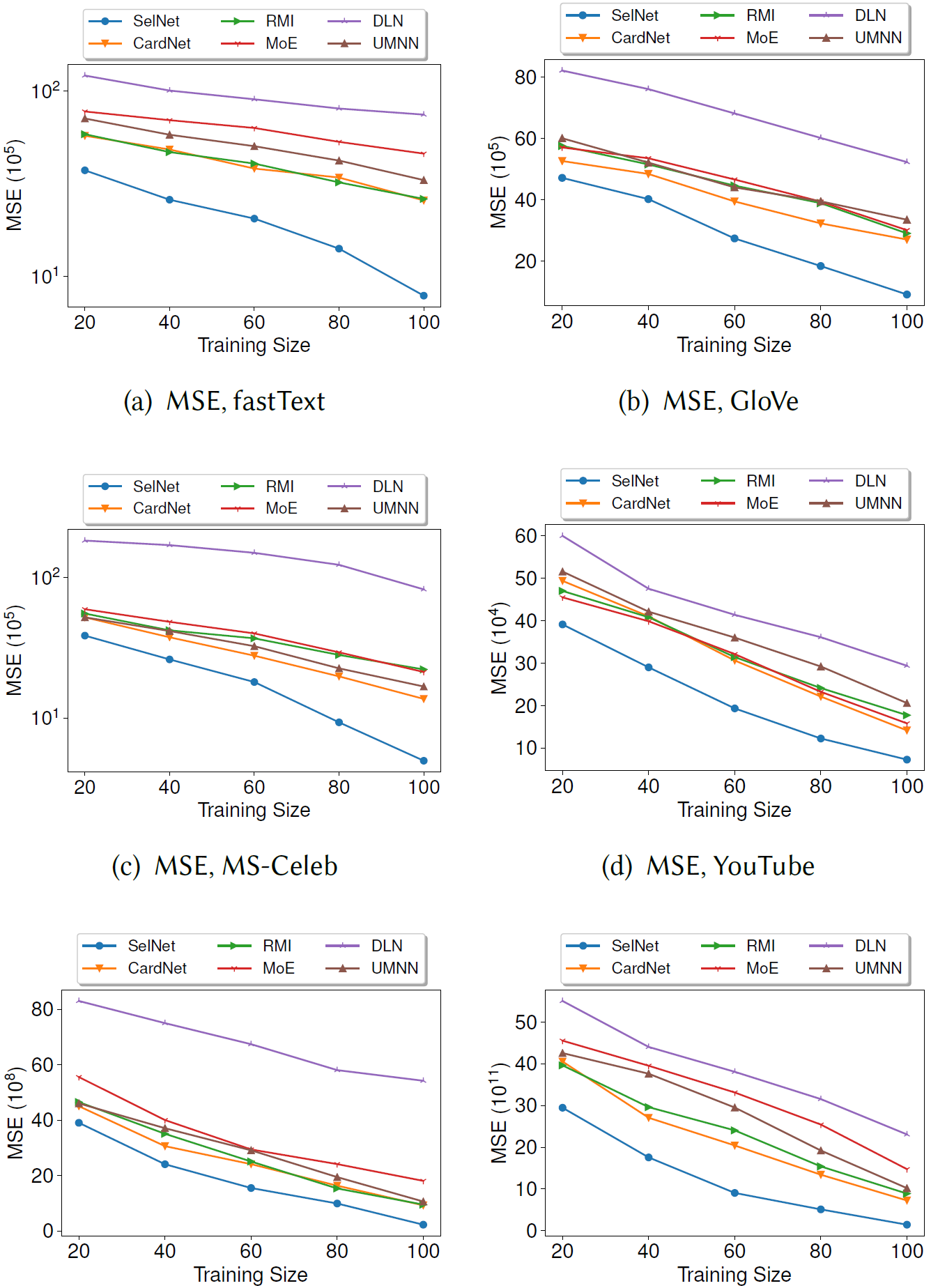
Figure 4: Varying training data size.

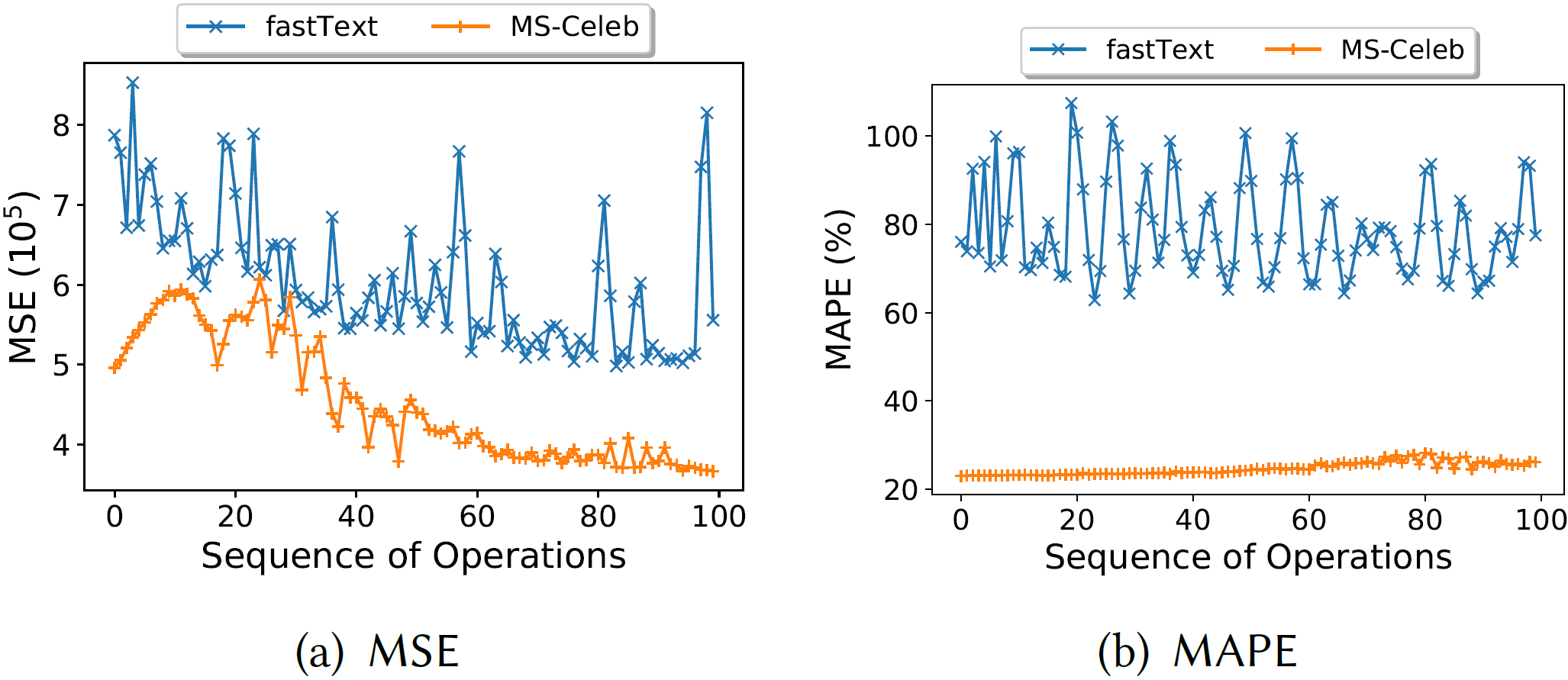
Figure 5: Data update.

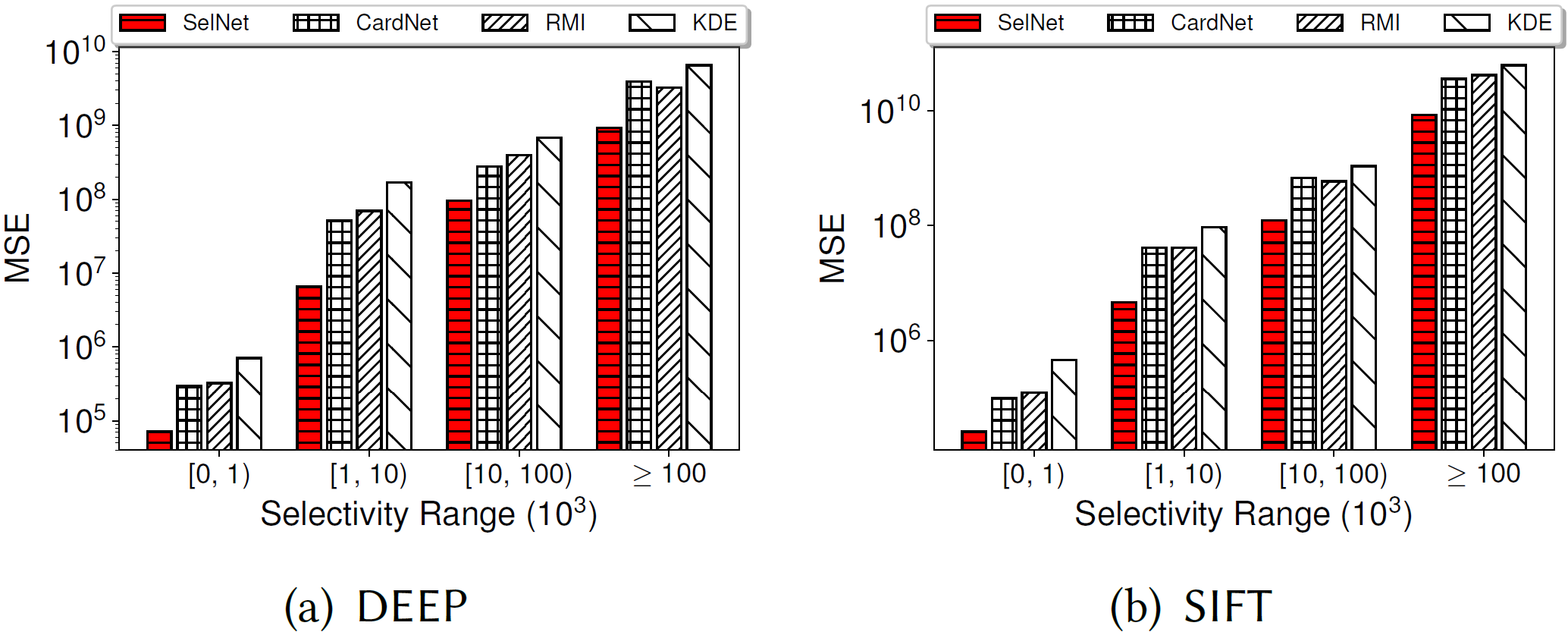
Figure 6: Generalizability

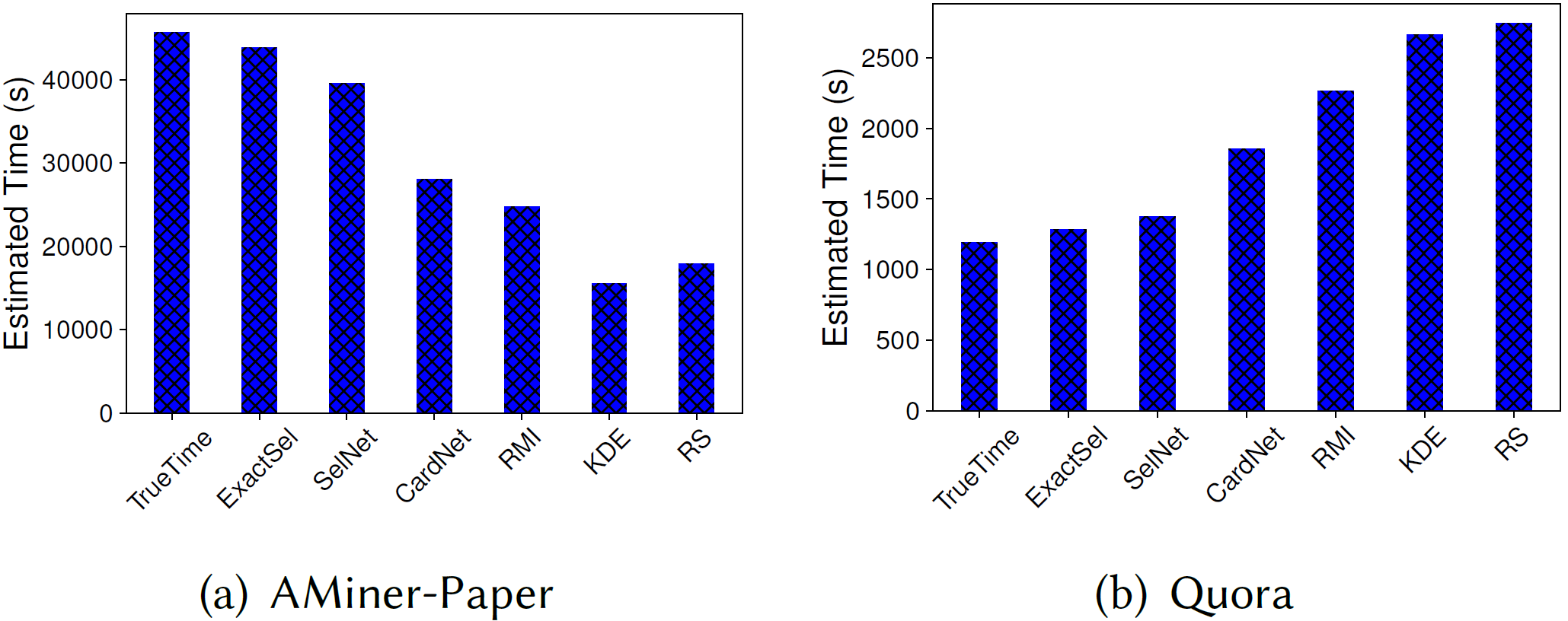
Figure 7: Estimated search time (10,000 queries).

Acknowledgements

This work was supported by NSFC 62072311 and U2001212, Guangdong Basic and Applied Basic Research Foun-dation 2019A1515111047 and 2020B1515120028, Guangdong Peral River Recruitment Program of Talents 2019ZT08X603, JSPS Kak-enhi 16H01722, 17H06099, 18H04093, and 19K11979, and ARC DPs 170103710 and 180103411.

Bibtex

@article{2020Consistent,

title={Consistent and Flexible Selectivity Estimation for High-dimensional Data},

author={ Wang, Y. and Xiao, C. and Qin, J. and Mao, R. and Zhang, R. },

journal={arXiv e-prints},

year={2020},

}

Downloads